I realise that I've never actually sat down and described my fully automated futures trading system in all it's detail; despite having runit for around 7.5 years now. That isn't because I want to keep it a secret - far from it! I've blogged or written books about all the various components of the system. Since I've made a fair few changes to my over the last year or so, it would seem to make sense to set down what the system looks like as of today.
You'll find reading this post much easier if you've already read my first book, "Systematic Trading". I'm expecting a christmas rush of book orders - I've bought all of my relatives copies, which I know they will be pleased to receive... for the 7th year in a row [Hope none of them are reading this, to avoid spoiling the 'surprise'!].
I'll be using snippets of code and configuration from my open source backtesting and trading engine, pysystemtrade. But you don't need to be a python or pystemtrade expert to follow along. Of course if you are, then you can find the full .yaml configuration of my system here. This code will run the system. Note that this won't work with the standard .csv supplied data files, since these don't include the 114 or so instruments in the config. But you can edit the instrument weights in the config to suit the markets you can actually trade.
In much of this post I'll also be linking to other blog posts I've written - no need to repeat myself ad infinitum.
I'll also be mentioning various data providers and brokers in this post. It's important to note that none of them are paying me to endorse them, and I have no connection with them apart from being a (reasonably) satisfied customer. In fact I'm paying them.... sadly.
Update: 5th January 2022, added many more instruments
Research summary
- Heuristic dynamic optimisation
- Dynamic optimisation using a grid search
- Fitting forecast weight by instrument and asset class (too complex!)
- Setting risk using drawdown levels (too simple!)
- A risk overlay (actually was in my old system, but not yet in my new system - a change I plan to make soon)
- Kurtosis as a trading rule (too complex and didn't work as well as expected)
- Dynamic optimisation using minimum tracking error (here and here)
- A systematic method for choosing instruments to trade or not
- Changing behaviour of rules when vol changes
- Handcrafting in it's automated variant
- Improving handcrafting correlation estimate adjustments and Sharpe Ratio estimate adjustments
- Estimating vol using a partially mean reverting method
- Skew as a trading rule
- Various other trading rules (no blog posts - read the book I'm currently writing and hope will come out next year!)
Which markets should we sample / trade
- Periodically survey the list of markets offered by my broker, interactivebrokers
- Create a list of markets I want to add data for. Gradually work my way through them (as of writing this post, my wish list has 64 instruments in it!)
- Regardless of whether I think I can actually trade them (see below), backfill their data using historic data from barchart.com
- Add them to my system, where I will start sampling their prices
- At this stage I won't be trading them until they're manually added to my system configuration
Because of the dynamic optimisation that my system uses, it's possible for me to calculate optimal positions for instruments that I can't / won't actually trade. And in any case, one might want to include such markets when backtesting - more data is always better!
I do however ignore the following markets when backtesting:
- Markets for which I have a duplicate (normally a different sized contract eg SP500 emini and micro; but could be a market traded in a different exchange) and where the duplicate is better. See this report.
- A couple of other markets where my data is just a bit unreliable (I might delete these instruments at some point unless things improve)
- The odd market which is so expensive I can't even just hold a constant position (i.e. the rolling costs alone are too much)
Then for trading purposes I ignore:
- Markets for which there are legal restrictions on me trading (for me right now, US equity sector futures; but could be eg Bitcoin for UK traders who aren't considered MiFID professionals)
- Markets which don't meet my requirements for costs and liqiuidity (again see here). This is why I sample markets for a while before trading them, to get an idea of their likely bid-ask spreads and hence trading costs
Which trading rules to use
- Momentum - EWMAC (See my first or third book)
- Breakout (blogpost)
- Relative (cross sectional within asset class) momentum (blogpost)
- Assettrend: asset class momentum (blogpost)
- Normalised momentum (blogpost)
- Acceleration
Trading rule performance
Here are the crude Sharpe Ratios for each trading rule:
breakout10 -1.19
breakout20 0.06
breakout40 0.57
breakout80 0.79
breakout160 0.79
breakout320 0.77
relmomentum10 -1.86
relmomentum20 -0.46
relmomentum40 0.01
relmomentum80 0.13
mrinasset160 -0.63
carry10 0.90
carry30 0.92
carry60 0.95
carry125 0.93
assettrend2 -0.94
assettrend4 -0.15
assettrend8 0.33
assettrend16 0.65
assettrend32 0.70
assettrend64 0.62
normmom2 -1.23
normmom4 -0.22
normmom8 0.41
normmom16 0.76
normmom32 0.82
normmom64 0.75
momentum4 -0.17
momentum8 0.46
momentum16 0.75
momentum32 0.78
momentum64 0.73
relcarry 0.37
skewabs365 0.52
skewabs180 0.42
skewrv365 0.22
skewrv180 0.33
accel16 -0.08
accel32 0.06
accel64 0.18
mrwrings4 -0.94I say crude, because I've just taken the average performance weighting all instruments equally. In particular that means we might have a poor performance for a rule that trades quickly because I've used the performance from many expensive instruments which wouldn't actually have an allocation to that rule at all. I've highlighted these in italics. In bold are the rules that are genuine money losers:
- mean reversion in the wings
- mean reversion across assset classes
Vol attenuation
As discussed here for momentum like trading rules we see much worse performance when volatility rises. For these rules, I reduce the size of the forecast if volatility is higher than it's historic levels. The code that does that is here.
Forecast weights
weights = dict(trendy = 0.6,other = 0.4)weights = dict(
assettrend= 0.15,
relmomentum= 0.12,breakout= 0.12,
momentum= 0.10,
normmom2= 0.11,skew= 0.04,
carry= 0.18,
relcarry= 0.08,
mr= 0.04
accel= 0.06)weights = dict(
assettrend2= 0.015,
assettrend4= 0.015,
assettrend16= 0.03,
assettrend32= 0.03,
assettrend64= 0.03,
assettrend8= 0.03,
relmomentum10= 0.02,
relmomentum20= 0.02,
relmomentum40= 0.04,
relmomentum80= 0.04,
breakout10= 0.01,
breakout20= 0.01,
breakout40= 0.02,
breakout80= 0.02,
breakout160= 0.03,
breakout320= 0.03,
momentum4= 0.005,
momentum8= 0.015,
momentum16= 0.02,
momentum32= 0.03,
momentum64= 0.03,
normmom2= 0.01,
normmom4= 0.01,
normmom8= 0.02,
normmom16= 0.02,
normmom32= 0.02,
normmom64= 0.03,
skewabs180= 0.01,
skewabs365= 0.01,
skewrv180= 0.01,
skewrv365= 0.01,
carry10= 0.04,
carry125= 0.05,
carry30= 0.04,
carry60= 0.05,
relcarry= 0.08,
mrinasset160= 0.02,
mrwrings4= 0.02,
accel16= 0.02,
accel32= 0.02,
accel64= 0.02
)
Next all I have to do is exclude any rules which a particular instrument can't trade because the costs exceed my 'speed limit' of 0.01 SR units. So here for example are the weights for an expensive instrument, Eurodollar with zeros removed:
EDOLLAR:
assettrend32: 0.048
assettrend64: 0.048
breakout160: 0.048
breakout320: 0.048
breakout80: 0.032
carry10: 0.063
carry125: 0.079
carry30: 0.063
carry60: 0.079
momentum32: 0.048
momentum64: 0.048
mrinasset160: 0.032
mrwrings4: 0.032
normmom32: 0.032
normmom64: 0.048
relcarry: 0.127
relmomentum80: 0.063
skewabs180: 0.016
skewabs365: 0.016
skewrv180: 0.016
skewrv365: 0.016
Forecast diversification multipliers will obviously be different for each instrument, and these are estimated using by standard method.
Position scaling: volatility calculation
Instrument performance and characteristics
Instrument weights
{'Ags': 0.15, 'Bond & STIR': 0.19, 'Equity': 0.22, 'FX': 0.13,
'Metals & Crypto': 0.13, 'OilGas': 0.13,
'Vol': 0.05}
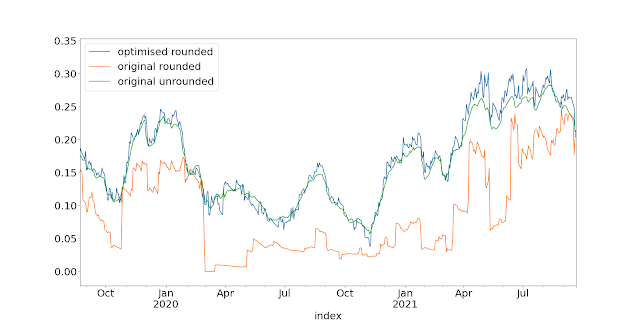
Dynamic optimisation
- Markets for which there are legal restrictions on me trading (for me right now, US equity sector futures; but could be eg Bitcoin for UK traders who aren't considered MiFID professionals)
- Markets which don't meet my requirements for costs and liqiuidity (again see here)
Backtest properties
('min', '-13.32'), ('max', '11.26'), ('median', '0.09578'), ('mean', '0.1177'), ('std', '1.44'),
('ann_mean', '30.11'), ('ann_std', '23.04'),
('sharpe', '1.307'), ('sortino', '1.814'), ('avg_drawdown', '-9.205'), ('time_in_drawdown', '0.9126'), ('calmar', '0.7017'), ('avg_return_to_drawdown', '3.271'), ('avg_loss', '-0.9803'), ('avg_gain', '1.06'), ('gaintolossratio', '1.081'), ('profitfactor', '1.26'), ('hitrate', '0.5383'), ('t_stat', '9.508'), ('p_value', '2.257e-21')[[('min', '-21.84'), ('max', '45.79'), ('median', '2.175'), ('mean', '2.55'), ('std', '7.768'), ('skew', '0.9368'), ('ann_mean', '30.55'), ('ann_std', '26.91'), ('sharpe', '1.135'), ('sortino', '2.177'), ('avg_drawdown', '-5.831'), ('time_in_drawdown', '0.6485'), ('calmar', '0.8371'), ('avg_return_to_drawdown', '5.239'), ('avg_loss', '-4.465'), ('avg_gain', '6.741'), ('gaintolossratio', '1.51'), ('profitfactor', '2.527'), ('hitrate', '0.626'), ('t_stat', '8.193'), ('p_value', '1.457e-15')]