Skew and expected returns

Some bloke* once said "The most overlooked characteristic of a strategy is the expected skew of it's returns, i.e. how symmetrical they are"

* It was me. "Systematic Trading" page 40

Skew then is an important concept, and one which I find myself thinking about a lot. So I've decided to write a series of posts about skew, of which is the first.

In fact I've already written a substantive post on trend following and skew, so this post is sort of the prequel to that. This then is actually the second post in the series, but really it's the first, because you should read this one first. Don't tell me you're confused, I know for a fact everyone reading this is fine with the fact that the Star Wars films came out in the order 4,5,6,1,2,3,7,8,9.

In this post I'll talk about two things. Firstly I will (briefly) discuss the difficulties of measuring skew: yes it's my old favourite subject sampling variation. Secondly I'll talk (at great length) about how skew can predict expected returns by answering the following questions:

• Do futures with negative skew generally have higher returns than those with positive skew? (strategic allocation)
• Does this effect still hold when we adjust returns for risk (using standard deviations only)? (risk adjusted returns)
• Are these rewards because we're taking on more risk in the form of 
• Does an asset that currently has negative skew outperform one that has positive skew? (time series and forecasting)
• Does an asset with lower skew than normal perform better than average (normalised time series)?
• Do these effects hold within asset classes? (relative value)

Some of these are well known results, others might be novel (I haven't checked - this isn't an academic paper!). In particular, this is the canonical paper on skew for futures: but it focuses on commodity futures. There has also been research in single equities that might be relevant (or it may not "Aggregate stock market returns display negative skewness. Firm-level stock returns display positive skewness." from here).

This is the sort of 'pre-backtest' analysis that you should do with a new trading strategy idea, to get a feel for it. What we need to be wary of is implicit fitting; deciding to pursue certain variations and not others having seen the entire sample. I will touch on this again later.

I will assume you're already familiar with the basics of skew, if you're not then you can (i) read "Systematic Trading" (again), (ii) read the first part of this post, or (iii) use the magical power of the internet, or if you're desperate (iv) read a book on statistics.

Variance in skew sample estimates

Really quick reminder: The variance in a sample estimate tells us how confident we can be in a particular estimate of some property. The degree of confidence depends on how much data we have (more data: more confident), the amount of variability in the data (e.g. for sample means, less volatility: more confident), and the estimator we are using (estimates of standard deviation: low variation)

We can estimate sampling distributions in two ways: using closed form formulae, or using a monte carlo estimator.

Closed form formulae are available for things like mean, standard deviation, Sharpe ratio and correlation estimates; but they usually assume i.i.d. returns (Gaussian and serially uncorrelated). For example, the formula for the variance of the mean estimate is sigma / N^2, where sigma is the sample variance estimate and N is the number of data points.

What is the closed form formula for skew? Well, assuming Gaussian returns the formula is as follows:

Skew = 0

Obviously that isn't much use! To get a closed form we'd need to assume our returns had some other distribution. And the closed forms tend to be pretty horific, and also the distributions aren't normally much use if there are outliers (something which, as we shall see, has a fair old effect on the variance). So let's stick to using monte carlo.

Obviously to do that, we're going to need some data. Let's turn to my sadly neglected open source project, pysystemtrade.

import numpy as np

from systems.provided.futures_chapter15.estimatedsystem import *
system = futures_system()

del(system.config.instruments) # so we can get results for everything
instrument_codes = system.get_instrument_list()

percentage_returns = dict()

for code in instrument_codes:
    denom_price = system.rawdata.daily_denominator_price(code)
    instr_prices = system.rawdata.get_daily_prices(code)

    num_returns = instr_prices.diff()
    perc_returns = num_returns / denom_price.ffill()

    # there are some false outliers in the data, let's remove them
    vol_norm_returns = system.rawdata.norm_returns(code)
    perc_returns[abs(vol_norm_returns)>10]=np.nan


    percentage_returns[code] = perc_returns

We'll use this data throughout the rest of the post; if you want to analyse your own data then feel free to substitute it in here.

Pandas has a way of measuring skew:

percentage_returns["VIX"].skew()
0.32896199946754984

We're ignoring for now the question of whether we should use daily, weekly or whatever returns to define skew.


However this doesn't capture the uncertainty in this estimate. Let's write a quick function to get that information:

import random

def resampled_skew_estimator(data, monte_carlo_count=500):
    """    Get a distribution of skew estimates
    :param data: some time series    :param monte_carlo_count: number of goes we monte carlo for    :return: list    """
    skew_estimate_distribution = []
    for _notUsed in range(monte_carlo_count):
        resample_index = [int(random.uniform(0,len(data))) for _alsoNotUsed in range(len(data))]
        resampled_data = data[resample_index]
        sample_skew_estimate = resampled_data.skew()
        skew_estimate_distribution.append(sample_skew_estimate)

    return skew_estimate_distribution

Now I can plot the distribution of the skew estimate for an arbitrary market:

import matplotlib.pyplot as pyplot

data = percentage_returns['VIX']
x=resampled_skew_estimator(data, 1000)
pyplot.hist(x, bins=30)

Boy... that is quite a range. It's plausible that the skew of VIX (one of the most positively skewed assets in my dataset) could be zero. It's equally possible it could be around 0.6. Clearly we should be quite careful about interpreting small differences in skew as anything significant.

Let's look at the distribution across all of our different futures instruments

# do a boxplot for everything

import pandas as pd

df_skew_distribution = dict()
for code in instrument_codes:
    print(code)
    x = resampled_skew_estimator(percentage_returns[code],1000)
    y = pd.Series(x)
    df_skew_distribution[code]=y

df_skew_distribution = pd.DataFrame(df_skew_distribution)

df_skew_distribution = df_skew_distribution.reindex(df_skew_distribution.mean().sort_values().index, axis=1)

df_skew_distribution.boxplot()
pyplot.xticks(rotation=90)

It looks like:

• Most assets are negatively skewed
• Positively skewed assets are kind of logical: V2X, VIX (vol), JPY (safe haven currency), US 10 year, Eurodollar (bank accounts backed by the US government). 
• The most negatively skewed assets include stock markets and carry currencies (like MXP, AUD) but also some commodities
• Several pinches of salt should be used here as very few assets have statistically significant skew in eithier direction.
• More negatively and positively skewed assets have wider confidence intervals
• Positive skewed assets have a postively skewed estimate for skew; and vice versa for negative skew
• There are some particularly fat tailed assets whose confidence intervals are especially wide: Corn, V2X, Eurodollar, US 2 year. 

Bear in mind that not all instruments have the same length of data, and in particular many do not include 2008.

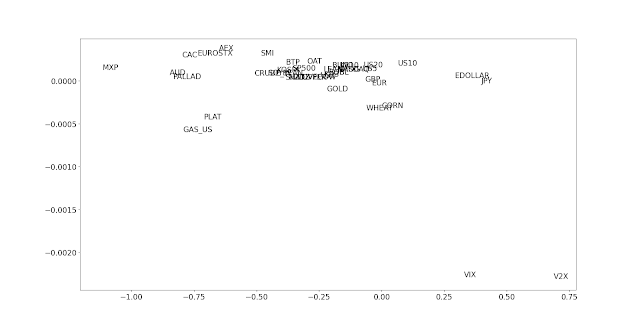
Do assets with negative skew generally have higher returns than those with positive skew? 

Let's find out.

# average return vs skew

avg_returns = [percentage_returns[code].mean() for code in instrument_codes]
skew_list = [percentage_returns[code].skew() for code in instrument_codes]

fig, ax = pyplot.subplots()
ax.scatter(skew_list, avg_returns, marker="")

for i, txt in enumerate(instrument_codes):
    ax.annotate(txt, (skew_list[i], avg_returns[i]))

Ignoring the two vol markets, it looks like there might be a weak relationship there. But there is huge uncertainty in return estimates. Let's bootstrap the distribution of mean estimates, and plot them with the most negative skew on the left and the most positive skew on the right:

def resampled_mean_estimator(data, monte_carlo_count=500):
    """    Get a distribution of mean estimates
    :param data: some time series    :param monte_carlo_count: number of goes we monte carlo for    :return: list    """
    mean_estimate_distribution = []
    for _notUsed in range(monte_carlo_count):
        resample_index = [int(random.uniform(0, len(data))) for _alsoNotUsed in range(len(data))]
        resampled_data = data[resample_index]
        sample_mean_estimate = resampled_data.mean()
        mean_estimate_distribution.append(sample_mean_estimate)

    return mean_estimate_distribution


df_mean_distribution = dict()
for code in instrument_codes:
    print(code)
    x = resampled_mean_estimator(percentage_returns[code],1000)
    y = pd.Series(x)
    df_mean_distribution[code]=y

df_mean_distribution = pd.DataFrame(df_mean_distribution)

df_mean_distribution = df_mean_distribution[df_skew_distribution.columns]

df_mean_distribution.boxplot()
pyplot.xticks(rotation=90)

Again, apart from the vol, hard to see much there. Let's lump together all the countries with above average skew (high skew), and those with below average (low skew):

skew_by_code = df_skew_distribution.mean()
avg_skew = np.mean(skew_by_code.values)
low_skew_codes = list(skew_by_code[skew_by_code<avg_skew].index)
high_skew_codes = list(skew_by_code[skew_by_code>=avg_skew].index)

def resampled_mean_estimator_multiple_codes(percentage_returns, code_list, monte_carlo_count=500):
    """
    :param percentage_returns: dict of returns    :param code_list: list of str, a subset of percentage_returns.keys    :param monte_carlo_count: how many times    :return: list of mean estimtes    """
    mean_estimate_distribution = []
    for _notUsed in range(monte_carlo_count):
        # randomly choose a code        code = code_list[int(random.uniform(0, len(code_list)))]
        data = percentage_returns[code]
        resample_index = [int(random.uniform(0,len(data))) for _alsoNotUsed in range(len(data))]
        resampled_data = data[resample_index]
        sample_mean_estimate = resampled_data.mean()
        mean_estimate_distribution.append(sample_mean_estimate)

    return mean_estimate_distribution


df_mean_distribution_multiple = dict()
df_mean_distribution_multiple['High skew'] = resampled_mean_estimator_multiple_codes(percentage_returns,high_skew_codes,1000)
df_mean_distribution_multiple['Low skew'] = resampled_mean_estimator_multiple_codes(percentage_returns,low_skew_codes,1000)

df_mean_distribution_multiple = pd.DataFrame(df_mean_distribution_multiple)
df_mean_distribution_multiple.boxplot()

Incidentally I've truncated the plots here because there is a huge tail of negative returns for high skew: basically the vol markets. The mean and medians are instructive, multiplied by 250 to annualise the mean return is -6.6% for high skew and +1.8% for low skew. Without that long tail having such an impact the medians are much closer: +0.9% for high skew and +2.2% for low skew.

If I take out the vol markets I get means of 0.6% and 1.7%, and medians of 1.2% and 2.3%. The median is unaffacted, but the ridiculously low mean return for high vol markets is taken out.

So: there is something there, of the order of a 1.0% advantage in extra annual returns for owning markets with lower than average skew. If you're an investor with a high tolerance for risk who can't use leverage; well you can stop reading now.

Does this effect still hold when we adjust returns for risk (using standard deviations only)?

Excellent question. Let's find out.

# sharpe ratio  vs skew

sharpe_ratios = [16.0*percentage_returns[code].mean()/percentage_returns[code].std() for code in instrument_codes]
skew_list = [percentage_returns[code].skew() for code in instrument_codes]

fig, ax = pyplot.subplots()
ax.scatter(skew_list, sharpe_ratios, marker="")
for i, txt in enumerate(instrument_codes):
    ax.annotate(txt, (skew_list[i], sharpe_ratios[i]))

Hard to see any relationship here, although the two vol markets still stand out as outliers.

Let's skip straight to the high skew/low skew plot, this time for Sharpe Ratios:

def resampled_SR_estimator_multiple_codes(percentage_returns, code_list, monte_carlo_count=500, avoiding_vol=False):
    """
    :param percentage_returns: dict of returns    :param code_list: list of str, a subset of percentage_returns.keys    :param monte_carlo_count: how many times    :return: list of SR estimtes    """
    SR_estimate_distribution = []
    for _notUsed in range(monte_carlo_count):
        # randomly choose a code        # comment in these lines to avoid vol        if avoiding_vol:
            code = "VIX"            while code in ["VIX", "V2X"]:
                code = code_list[int(random.uniform(0, len(code_list)))]
        else:
            code = code_list[int(random.uniform(0, len(code_list)))]

        data = percentage_returns[code]
        resample_index = [int(random.uniform(0,len(data))) for _alsoNotUsed in range(len(data))]
        resampled_data = data[resample_index]
        SR_estimate = 16.0*resampled_data.mean()/resampled_data.std()
        SR_estimate_distribution.append(SR_estimate)

    return SR_estimate_distribution

df_SR_distribution_multiple = dict()
df_SR_distribution_multiple['High skew'] = resampled_SR_estimator_multiple_codes(percentage_returns,high_skew_codes,1000)
df_SR_distribution_multiple['Low skew'] = resampled_SR_estimator_multiple_codes(percentage_returns,low_skew_codes,1000)

df_SR_distribution_multiple = pd.DataFrame(df_SR_distribution_multiple)
df_SR_distribution_multiple.boxplot()

Hard to see what, if any, is the difference there. The summary statistics are even more telling:

Mean: High skew 0.22, Low skew 0.26
Median: High skew 0.22, Low skew 0.20

Once we adjust for risk, or at least risk measured by the second moment of the distribution, then uglier skew (the third moment) doesn't seem to be rewarded by an improved return.

Things get even more interesting if we remove the vol markets again:

Mean: High skew 0.37, Low skew 0.24
Median: High skew 0.29, Low skew 0.17

A complete reversal! Probably not that significant, but a surprising turn of events none the less.

Does an asset that currently has negative skew outperform one that has positive skew? (time series and forecasting)

Average skew and average returns aren't that important or interesting; but it would be cool if we could use the current level of skew to predict risk adjusted returns in the following period.

An open question is, what is the current level of skew? Should we use skew defined over the last week? Last month? Last year? I'm going to check all of these, since I'm a big fan of time diversification for trading signals.

I'm going to get the distribution of risk adjusted returns (no need for bootstrapping) for the following N days, where skew over the previous N days has been higher or lower than average. Then I do a t-test to see if the realised Sharpe Ratio is statistically significantly better in a low skew versus high skew environment.

all_SR_list = []
all_tstats=[]
all_frequencies = ["7D", "14D", "1M", "3M", "6M", "12M"]

for freqtouse in all_frequencies:
    all_results = []
    for instrument in instrument_codes:
            # we're going to do rolling returns            perc_returns = percentage_returns[instrument]
            start_date = perc_returns.index[0]
            end_date = perc_returns.index[-1]

            periodstarts = list(pd.date_range(start_date, end_date, freq=freqtouse)) + [
                end_date]

            for periodidx in range(len(periodstarts) - 2):
                # avoid snooping                p_start = periodstarts[periodidx]+pd.DateOffset(-1)
                p_end = periodstarts[periodidx+1]+pd.DateOffset(-1)
                s_start = periodstarts[periodidx+1]
                s_end = periodstarts[periodidx+2]

                period_skew = perc_returns[p_start:p_end].skew()
                subsequent_return = perc_returns[s_start:s_end].mean()
                subsequent_vol = perc_returns[s_start:s_end].std()
                subsequent_SR = 16*(subsequent_return / subsequent_vol)

                if np.isnan(subsequent_SR) or np.isnan(period_skew):
                    continue                else:
                    all_results.append([period_skew, subsequent_SR])

    all_results=pd.DataFrame(all_results, columns=['x', 'y'])
    avg_skew=all_results.x.median()
    all_results[all_results.x>avg_skew].y.median()
    all_results[all_results.x<avg_skew].y.median()

    subsequent_sr_distribution = dict()
    subsequent_sr_distribution['High_skew'] = all_results[all_results.x>=avg_skew].y
    subsequent_sr_distribution['Low_skew'] = all_results[all_results.x<avg_skew].y


    subsequent_sr_distribution = pd.DataFrame(subsequent_sr_distribution)

    med_SR =subsequent_sr_distribution.median()
    tstat = stats.ttest_ind(subsequent_sr_distribution.High_skew, subsequent_sr_distribution.Low_skew, nan_policy="omit").statistic
    all_SR_list.append(med_SR)
    all_tstats.append(tstat)

all_tstats = pd.Series(all_tstats, index=all_frequencies)
all_tstats.plot()

Here are the T-statistics:

Large negative numbers mean a bigger difference in performance. It looks like we get significant results measuring skew over at least the last 1 month or so.

How much is this worth to us? Here are the conditional median returns:

all_SR_list = pd.DataFrame(all_SR_list, index=all_frequencies)
all_SR_list.plot()

Nice. An extra 0.1 to 0.4 Sharpe Ratio units. One staggering thing about this graph is this, when measuring skew over the last 3 to 12 months, assets with higher than average skew make basically no money.

Should we use 'lower than average skew' or 'negative skew' as our cutoff / demeaning point?

Up to now we've been using the median skew as our cutoff (which in a contionous trading system would be our demeaning point, i.e. we'd have positive forecasts for skew below the median, and negative forecasts for skew which was above). This cuttoff hasn't quite been zero, since on average more assets have negative skew. But is there something special about using a cutoff of zero?

Easy to check:

#avg_skew=all_results.x.median()# instead:

avg_skew = 0

With a less symettric split we'd normally to get better statistical significance (since the 'high skew' group is a bit smaller now), however the results are almost tthe same. Personally I'm going to stick to using the median as my cutoff, since it will make my trading system more symettric.

Does an asset with lower skew than normal perform better than average (normalised time series)?

The results immediately above can be summarised as:

- Assets which currently have more negative skew than average - measured as an average across all assets over all time

This confound three possible effects:

- Assets with on average (over all time) more negative skew perform better on average (the first thing we checked - and on a risk adjusted basis the effect is pretty weak and mostly confined to the vol markets)
- Assets which have currently more negative skew than their own average perform better
- Assets which currently have more negative skew than the current average perform better than other assets

Let's check two and three.

First let's check the second effect, which can be rephrased as is skew demeaned by the average for an asset predictive of future performance for that asset?
I'm going to use the average skew for the last 10 years to demean each asset.

Code the same as above, except:

perc_returns = percentage_returns[instrument]
all_skew = perc_returns.rolling("3650D").skew()

...

period_skew = perc_returns[p_start:p_end].skew()
avg_skew = all_skew[:p_end][-1]
period_skew = period_skew - avg_skew
subsequent_return = perc_returns[s_start:s_end].mean()

Similar to before, but not quite as significant. The weaker effect at one month has vanished. Here are the Sharpe Ratios:

The 'skew bonus' has reduced somewhat to around 0.2 SR points for the last 12 months of returns.

Now let's check the third effect, which can be rephrased as is skew demeaned by the average of current skews across all assets asset predictive of future performance for that asset?

Code changes:

all_SR_list = []
all_tstats=[]
all_frequencies = ["7D", "14D", "30D", "90D", "180D", "365D"]

...

for freqtouse in all_frequencies:
    all_results = []
    # relative value skews need averaged
    skew_df = {}
    for instrument in instrument_codes:
        # rolling skew over period        instrument_skew = percentage_returns[instrument].rolling(freqtouse).skew()
        skew_df[instrument] = instrument_skew

    skew_df_all = pd.DataFrame(skew_df)
    skew_df_median = skew_df_all.median(axis=1)

    for instrument in instrument_codes:

....

period_skew = perc_returns[p_start:p_end].skew()
avg_skew = skew_df_median[:p_end][-1]
period_skew = period_skew - avg_skew
subsequent_return = perc_returns[s_start:s_end].mean()
...

Plots, as before:

To summarise then:

- Using recent skew is very predictive of future returns, if 'recent' means using at least 1 month of returns, and ideally more. The effect is strongest if we use the last 6 months or so of returns.
- Some, but not all, of this effect persists if we normalise skew by the long run average for an asset. So, for example, even for assets which generally have positive skew, you're better off investing in them when their skew is lower than normal
- Some, but not all, of this effect persists if we normalise skew by the current average level of skew. So, for example, even in times when skew generally is negative (2008 anyone?) it's better to invest in the assets with the most negative skew.

We could formally decompose the above effects with for example a regression, but I'm more of a fan of using simple trading singles which are linearly weighted, with weights conditional on correlations between signals.

Do these effects hold within asset classes? (relative value)

Rather than normalising skew by the current average across all assets, maybe it would be better to consider the average for that asset class. So we'd be comparing S&500 current skew with Eurostoxx, VIX with V2X, and so on.

all_SR_list = []
all_tstats=[]
all_frequencies = ["7D", "14D", "30D", "90D", "180D", "365D"]
asset_classes = list(system.data.get_instrument_asset_classes().unique())

for freqtouse in all_frequencies:
    all_results = []
    # relative value skews need averaged
    skew_df_median_by_asset_class = {}
    for asset in asset_classes:
        skew_df = {}
        for instrument in system.data.all_instruments_in_asset_class(asset):
            # rolling skew over period            instrument_skew = percentage_returns[instrument].rolling(freqtouse).skew()
            skew_df[instrument] = instrument_skew

        skew_df_all = pd.DataFrame(skew_df)
        skew_df_median = skew_df_all.median(axis=1)
        # will happen if only one asset class        skew_df_median[skew_df_median==0] = np.nan

        skew_df_median_by_asset_class[asset] = skew_df_median

    for instrument in instrument_codes:
            # we're going to do rolling returns            asset_class = system.data.asset_class_for_instrument(instrument)

            perc_returns = percentage_returns[instrument]

...

period_skew = perc_returns[p_start:p_end].skew()

avg_skew = skew_df_median_by_asset_class[asset_class][:p_end][-1]
period_skew = period_skew - avg_skew
subsequent_return = perc_returns[s_start:s_end].mean()

That's interesting: the effect is looking a lot weaker except for the longer horizons. The worse t-stats could be explained by the fact that we have less data (long periods when only one asset is in an asset class and we can't calculate this measure), but the relatively small gap between Sharpe Ratios isn't affected by this.

So almost all of the skew effect is happening at the asset class level. Within asset classes, for futures at least, if you normalise skew by asset class level skew you get a not significant 0.1 SR units or so of benefit, and then only for fairly slow time frequencies.

Summary

This has been a long post. And it's been quite a heavy, graph and python laden, post. Let's have a quick recap:

• Most assets have negative skew
• There is quite a lot of sampling uncertainty around skew, which is worse for assets with outliers (high kurtosis) and extreme absolute skew
• Assets which on average have lower (more negative) skew will outperform in the long run.
• This effect is much smaller when we look at risk adjusted returns (Sharpe Ratios), and is driven mainly by the vol markets (VIX, V2X)
• Assets with lower skew right now will outperform those with higher skew right now. This is true for skew measuring and forecasting periods of at least 1 month, and is strongest around the 6 month period. In the latter case an average improvement of 0.4 SR units can be expected.
• This effect is the same regardless of wether skew is compared to the median or compared to zero.
• This effect mostly persists even if we demean skew by the rolling average of skew for a given asset over the last 10 years: time series relative value
• This effect mostly persists if we deman skew by the average of current skews across all assets: cross sectional relative value
• But this effect mostly vanishes if the relative value measure is taken versus the average for the relevant asset class.

This is all very interesting, but it mostly compares, and it still isn't a trading strategy. So in the next post I will consider the implementation of these ideas as a suite of trading strategies: 

• Skew measured over the last N days, relative to a long term average across all assets
• Skew measured over the last N days, relative to a long term average for this asset
• Skew measured over the last N days, relative to the current average for all assets
• Skew measured over the last N days, relative to the current average for the relevant asset class

Where N will be in the ballpark 10... 250 business days.

For now it's important to bear in mind that I must not discard any of the above ideas because of likely poor performance:

• lower values of N (though some might be removed because their trading costs are too high), eg 2 weeks
• Asset class relative value

New book: Leveraged Trading

This month* marks the release of my third book, with the snappy title "Leveraged Trading", and the slightly less snappy subtitle "A professional approach to trading FX, stocks on margin, CFDs, spread bets and futures for all traders".

Photo courtesy of Harriman House. As you can see, the book makes an excellent books-stand for itself

* Official publication date is 29th October. Actually I finished the book in late August, and I've had print copies in my hand since mid September (and I know some other people have received their copies already), but for some reason I have never understood my books are always released at the end of October in odd numbered years (Systematic Trading 2015, Smart Portfolios 2017, Leveraged Trading 2019). Whether I stick to this schedule for book four is an open question.

You can order the book from the publishers, Harriman House, here (other, massive monopolistic online bookshops are available, but I get a better royalty if you buy direct from the publishers). There is plenty of information on my website, here.

This post is aimed at regular readers of my stuff who might be wondering if it's worth buying this third book (short answer: yes, of course! Even shorter and more honest answer: maybe!).

Where did the idea for this book come from?

Two sources of ideas really. The first was a constant stream of people telling me that they loved "Systematic Trading", but with two huge caveats. First caveat was the portfolio sizes in the book, which started at $100,000 and just kept on going up into seven and eight figures. The second caveat was that it was all just too hard and required far too much pre-existing technical knowledge. Classic amazon review "This won't not be the first book on systematic trading you buy, or even the tenth...". Thanks: I am not sure that even I own 9 other books about systematic trading!

Although I'd originally intended to write a book which was accessible to smaller retail traders my publisher and I decided that I'd be better off writing something more technical that was aimed at institutional traders. There is a bit of stuff about minimum capital in the latter part of the book but mostly I assume you have lots of money and lots of knowledge about the markets.

The second source of idea was my habit of watching "trading guru" youtube videos, or at least having them on in the background whilst I worked. I find these videos fascinating, but I also find it absolutely terrifying that these people are influencing tens or even hundreds of thousands of people. The more I watched these videos, the more I noticed when just walking around or surfing the internet the increasing levels of advertising from brokers peddling dangerously leveraged products. This was all pretty bad already, but when the Crypto currency hype got going in 2018 it reached another level. Over the last few years I've noticed more and more "ordinary" people asking me for advice which inevitable involves trading "four-ex" or Bitcoin.

I don't write books primarily for the money, I write them as a philanthropic gesture to help as many people as possible avoid the plethora of ways to get ripped off in the financial industry. It struck me that relatively inexperienced retail traders using leveraged products are a very large group of people who needed a large amount of help. Maybe I should write a book for them. So I did.

What is the main focus of the book and who is it for?

So the book is about safe leveraged trading. Regular readers will know that I frequently talk about the three main errors of systematic trading: overbetting (taking on too much risk), overtrading (trading too often), and overfitting. This book focuses mainly on dealing with the first two: getting the right level of leverage and the right frequency of trading. It does this by suggesting that novice traders use a system (quelle surprise!). The system is calibrated to avoid excessive risk or trading costs. I also explain how I designed the system to avoid the perils of overfitting.

But it's also a book for those who don't necessarily want to trade purely systematically. In my first book I introduced the idea of a "Semi-Automatic Trader"- someone who chooses which position to hold in some non systematic way, but sizes and closes positions systematically. I take this idea much further here, and explain in more detail how you can combine human intuition with the most useful parts of a trading system. Importantly, I also explain how you should calibrate your risk and trading frequency depending how well you have performed in live trading.

It's a book for relative beginners. As such it doesn't assume much knowledge and also goes into significant amounts of detail about specific leveraged products. I chose five products, because one is common in the US (margin trading), two are common in Europe but illegal for retail traders in the US (spread-bets and CFDs), and two are traded pretty much everywhere (futures and spot FX).

It's a book for traders without much money. A key theme throughout is answering the question "What is the best use of my scarce capital?". 

What specific advice is there for smaller traders?

Firstly I talk a lot about product choice. For reasons I explain in the book* there is generally an inverse relationship between the minimum capital required to trade something, and how much it costs to trade.

* If you must know: within product type and across instruments it's vol scaling. But also the more 'institutional' the product, the larger the capital required, the cheaper it is to trade. So futures are cheaper than CFDs for example.

So the optimum choice for a smaller trader is to find a relatively cheap product which they can afford to trade. That rules out most futures (too big) and also a lot of OTC products (too expensive).

If I assume that traders don't have much capital, and are relatively inexperienced, then it makes sense for their first trading system to be binary (no 'forecasts', which requires more capital to do properly), discrete (trades are opened and closed without any adjustment to position size), and close trades using a stop loss (which most people understand).

Then suppose you have slightly more than the bare minimum to trade: what next? Should you diversify by adding another instrument to your portfolio? Should you make your system more complex by adding new trading rules? Should you start trading a non binary system? All of these decisions are discussed, and viewed through the prism of a trader with limited capital.

Why the title, and the focus on leveraged trading?

A few reasons. As I've already said I think that the leveraged end of the OTC retail broker spectrum is one of the most dangerous parts of the trading world, even after the EU introduced restrictions on retail margin levels the availability of leverage is still far too generous. It's also a world to which naive punters are naturally attracted, due to the lottery like payoffs available ("invest £100 and win £10,000!") with massive leverage.

Secondly getting your leverage level right is probably one of the most important decisions any trader can make, and one most retail traders get spectacularly wrong. As an institutional trader your risk target is exogenous and usually fairly modest (even the 25% vol target I run at would be considered punchy in most shops). At a product level you're unlikely to have excessive leverage, unless it's something with really low vol (front contract EuroYen anyone?) or negative skew. But telling a retail trader that they should only use leverage of 1.5 rather than the 50 their broker will allow them is another story.

Thirdly, and very cynically, I didn't want to make this a "system trading" book as this would limit the audience. Of course I want more people to read this from a philanthropic point of view, and the money is a nice bonus (note book is also priced 50% lower than my first two books). I think fewer people are likely to pick up a book with "Systems" in the title than something that name-checks the CFDs and spread-bets that they've been hearing about in the news.

Finally from a technical point of view it's much easier to explain position sizing using inverse vol weighting if you can use leverage. You don't need to worry about risk appetite and the book can be 50-100 pages shorter.

I've already read "Systematic Trading". Should I bother with this?

That is an excellent question, and one I address in the book:

"You will see from my website that I wrote another trading book a few years ago: “Systematic Trading” (ST). Perhaps you are browsing on-line or in your local book shop and trying to decide which of these two books you should buy. Maybe you already own ST, and are considering adding this book, “Leveraged Trading” (LT), to your collection.

To help you decide, the main differences between the two books are:​

• As the title suggests, ST is mostly aimed at traders who are enthusiastic about systems trading. LT helps new traders learn how to trade by using a system, but then explains how to combine the system with their own human intuition; the method I’ve named “Semi-Automatic Trading”. 
• The trading systems in ST require large amounts of money (at least £100,000; around $130,000). The Starter System in LT needs just £1,100 or $1,500. I spend a lot of time in LT discussing how smaller traders can make best of their scarce capital.
• ST is written for relatively advanced traders with some prior knowledge of certain financial concepts. LT is suitable for novices.
• ST is a generic book which doesn’t go into much detail about individual markets. LT explains how to trade specific leveraged products.
• ST explains the various components of a complex trading system one by one; it isn’t until the book is finished that you can see the entire picture. In LT I introduce a simple system in its entirety which you can start using right away. I then go on to explain how, and why, you could make it more complicated.
• ST explains how to design trading systems from scratch, which requires using software to simulate historical system performance (a process called back-testing). In LT I present a system I have already back-tested. I then explain how you can modify the system for different types of trading, and to cover different markets, without needing any further testing.

 Because I have designed the trading systems in this book with the same principles in mind there are some ideas that readers of ST will find familiar, although there is no duplicated content in this book. I would recommend that you read “Leveraged Trading” (LT) if:

• You tried to read ST and didn’t get it.
• You read and understood ST but are struggling to build a simple system from scratch.
• You have not read ST and are an inexperienced trader who is unfamiliar with financial theory and back-testing software.
• You are specifically interested in trading leveraged products: FX, CFD, margin accounts, spread-bets, and futures.
• You do not have enough cash to trade the systems in ST.
• You are interested in combining your own trading intuition with a trading system: semi-automatic trading."

​

I am the guy who complained there weren't enough formulas in "Systematic Trading"

Just for you there are so many formulas in Leveraged Trading I lost count.

In all seriousness because this book is more 'hand-holding' it does go into more explicit detail and includes formulas. So for example where in Systematic Trading I might have just said "Take a weighted average" here I include the actual formula for a weighted average.

But don't panic, there are no greek letters* in the book, just simple formula that an 11 year old could understand.

* Full disclosure: there might be a few capital Sigma to indicate a summation. But definitely no integrals.

I am the guy who complained there weren't enough numerical examples in "Systematic Trading"

Again, you will love this book! It's my bet that beginners prefer to see concrete tangible examples rather than pages of theory.

I notice there is the usual obsession with costs

Yes! I make no apology for it. Costs are the only thing you can control and forecast (almost) perfectly. If you get your leverage right but trade too often then you will still go bust just a bit more slowly. Also there is a lot of misunderstanding and misinformation about costs out there. In particular brokers in the OTC world will usually promote the low levels of execution costs on non dated derivatives ("zero commission! 0.5 point spread!") whilst quietly hiding the very high levels of holding costs (17 clicks into the website you may just find that you are paying LIBOR+3% in overnight funding charges).

And talking about costs allows me to talk about one of my favourite bugbears: day trading. The idea that you can be profitable day trading, whilst paying retail level commissions and crossing the trading spread, is an idea that deserves to be rebutted constantly (if only to try and match the constant stream of BS from brokers and trading gurus promoting the concept).

There's also a bonus section in this book on reducing your costs through optimal execution tactics. You can find it in the appendix (it was a complete chapter, but was too short).

You really have it in for brokers and trading gurus, don't you?

Yes! Partly this makes the book more entertaining, for the same reason it's more fun to read a novel with a decent villain in it. But yes, I really hate the whole retail trading culture which enriches the shareholders of spreadbetting firms and a bunch of charlatans at the expense of emptying the accounts of generally less wealthy people who don't know any better. This strikes me as worth a different circle of hell compared to the institutional buy and sell side who are effectively payed through a pro-rata tax on everyone's managed money (a tax which you can reduce if you are smart and only invest in passive funds, or avoid overtrading: c.f. Smart Portfolios).

Of course I don't hate all brokers - only the ones that are expensive or dodgy. And not everyone who has ever written a book about trading is automatically dodgy, or that would clearly include me. But you should be extremely skeptical of any trading gurus who claim outlandish returns, who don't tell you what their trading returns are, who aren't open about their methodology, and whose videos mostly consist of them prancing around a villa in Thailand whilst occasionally pretending to trade.

You can rent this villa for your youtube videos here

Presumably as this is a 'beginners' book there is nothing in here about statistical uncertainty?

You couldn't be more wrong! I had to bring in statistical uncertainty so that people would understand why costs are important when selecting instruments and trading rules, and pre-cost returns irrelevant (since they are not statistically different from each other). I needed the concept to explain why diversification is so important (it gives you a massively statistically significant improvement in returns), whilst adding more trading rules and making your system more complex are good to do but not so valuable (the improvements are more modest and at times skate on the verge of insignificance).

Of course there is nothing in here about the mechanics of fitting, or in and out of sample periods, and you will not see the formulas for parameter uncertainty which I punish my students with every year. But I firmly believe that no trader will survive unless they have a good intuitive understanding of how uncertainty affects financial markets generally and trading strategies specifically.

Who helped you write this book?

The team at my publishers, Harriman House, were their usual brilliant selves. Craig Pearce was the commissioning editor and Stephen Eckett did the editing. I understand why people self publish, but I'm far too lazy and realistically I won't be able to match the professionalism of these guys. It's extremely difficult to be self critical enough to do a decent job of writing a book outline that is coherent and will reach the right audience. It's even more difficult to find someone who is able to read your stuff and give you intelligent feedback on everything from structure to content to grammar and spelling (and believe me, almost nobody can edit their own stuff).

(Anyone who compares my unedited blog and my edited books can clearly see the value of a decent editor)

As with previous books I had three "beta readers" who had to read the shockingly awful earlier drafts before Stephen had turned them into a readable book. Riccardo Ronco also read "Smart Portfolios" and did an equally excellent job with this book. James Udall filled in my not inconsiderable gaps in understanding about CFDs and spread bets. Finally Tomasz Mlynowski, whose day job involves (amongst other things) reading my lecture notes and explaining them to baffled students, brought along his fine toothed eye for errors and mixed metaphors.

Finally, it's a cliche, but writing is a job with flexible hours from which it's difficult to switch off. So it's tough living with a writer. So the three young people, one slightly older person, and cat, that live with me deserve a lot of credit.

Okay, maybe not the cat, which has a nasty habit of sitting on my lap when I am trying to finish a paragraph.

So.... book four?

Yes, probably. This will either be "Smart Portfolios for dummies" in the same way that this book is kind of "Leveraged Trading for dummies", or a more cerebral book on uncertainty in financial markets (which I know already my publisher will be less keen on). Before then however I will be working on another project- a new trading strategy - details to follow in the next blog post.