Capital correction (pysystemtrade)

This post is about how should you adjust the trading capital you have at risk given the profitability (or not) of your trading account.

I'm posting this for three reasons. Firstly it's a pretty important topic. I address, in some detail, how to set your risk target for a given amount of trading capital in chapter 9 of my book. I only briefly discuss what you should do thereafter, once the size of your account changes*.

* There was actually a lot more on this in an early draft of the book, but I had to do some drastic editing to get it down to a size when it could be lifted with one hand.

Secondly in my open python backtesting package pysystemtrade there has been as yet no facility for variable capital - the trading capital is fixed. I've lost count of the number of people* who have asked (a) if the capital is fixed, (b) why the capital is fixed, and (c) if I plan to modify the code so the capital changes over time. It's probably one of the most requested features (the others being the ability to pull in futures prices from quandl.com and stitch them... don't worry it's coming... eventually).

* Actually I haven't. As of the time of writing exactly eleven people have asked about this.

In the first part of this post I'll explain more about the difference between fixed and variable capital. The second part will discuss the different methods of adjusting capital that I think are reasonable to use. In the final part I'll show how to use the latest and greatest version of pysystemtrade to work with adjustable capital in it's various guises.

A very quick primer on capital

For those who haven't read my book let me briefly explain the concept of risk capital. We assume we're prepared to lose a certain amount of money, say $250,000 (I'm using US dollars, because according to Google most of the readers of this blog will shortly be living under the yoke of President Trump or Clinton). We then decide how much risk we want to take on that, which I measure in as an average of annualised volatility of returns over a long period. At 10% annualised risk, that would be $25,000, or around $1,560 per day. That figure is then used to scale our positions; if we doubled our risk capital our positions would also double.

This post then is essentially about whether the $250K is a fixed number or variable.

Fixed versus variable capital

If you understand the difference between simple and compound interest, then you already know the difference between fixed and variable risk capital. With fixed capital if you earn a 5% return on £100 (£5), and then lose 5% the next day (also £5), then you will be flat and still own £100. With variable capital you will earn a 5% return on day one, and then have £105. A 5% loss on day two starting with £105 is £5.25; bringing you down to £99.75.

This quote may be apocryphal. Einstein probably wasn't that into finance. Though had he been alive today, he'd probably have got a job as a quant in a Swiss investment bank instead of as a patent clerk. And he would never have had time to write ground breaking physics papers.
Source: http://www.rohitdhir.com/compounding-the-8th-wonder/ 

This is easily illustrated with a few pictures. Here I've generated 20 years of monthly random Gaussian returns in a spreadsheet, with an annualised Sharpe ratio of 1.0, and a standard deviation of 20%.

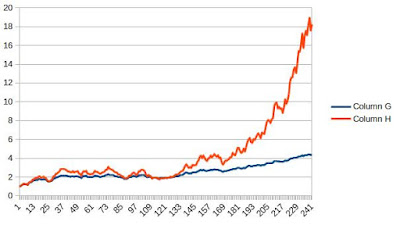Column G: Fixed capital, Column H: Variable capital

Column G: Fixed capital only to make the picture clearer

Column H: Log scale of variable capital

Notice that:

• The variable capital line grows much more than the fixed capital line.
• Over time the volatility of the variable capital line increases.
• On a log scale the variable capital line looks exactly like the fixed capital line; though the numbers on the y axis are different.

Traders who aren't used to the idea of targeting a particular risk level will usually think in terms of variable capital. If you're a long only unleveraged stock investor this makes complete sense; your risk level will naturally grow with the size of your investments unless you sell on gains to keep risk capital constant. Derivatives traders who don't have a full and complete understanding of the right way to do money management often trade arbitrary sizes, low to begin with and then step suddenly, or pyramid up on individual positions. For them risk capital will be all over the place.

Notice here that I'm assuming that the variable capital grows and shrinks with the percentage returns that we're making. I'll look at a different ways of doing capital correction later in the post.

Why looking at constant capital account curves usually makes sense...

I find it extremely difficult to look at variable capital lines. Returns are barely visible at the start of the backtest, and look scarily huge at the end. They are fine for short backtests of a few years (unless you have a very high risk target and /or performance in which case compounding will happen quicker). However you need decades of data to have confidence in your performance.

Take for example the drawdown that happens around month 210 in the simple excel charts above. On the variable capital line this looks as severe as the earlier drawdowns such as the one up to month 85. But in reality it's nowhere near as bad.

It's for this reason that pysystemtrade up to now has used fixed capital (and will continue to do so apart from a few extra methods I'll discuss below).

When variable capital might make sense

As far as I can tell the only reason you would want to use variable capital is to fantasise about how rich you will be if you run your system for 20 years; and how you'll be pushing around the Eurodollar market with the thousands of contracts you'll need to trade (see below for more on this).

The other reason you might use variable capital in a backtest is to test out your chosen method for capital correction, and see what effect it has. Again, more on these below.

It might also make sense if you want to know if your bet size is Kelly optimal, in which case you'd want to generate variable account curves using different leverage, and pick the one with the highest terminal account value (which is equivalent to the maximum log utility or geometric mean). This is a lot of unnecessary work and will probably result in you having too much risk, rather you should use the rule of thumb based on the Sharpe ratio and skew I discuss briefly here, and in more detail in chapter 9 of my book.

Live trading

In live trading you're probably going to want to use some kind of variable capital. The main reason for this is that the first rule of money management is to scale your risk down when you lose money. The famous Kelly criteria implies that if you lose 10% of your money, you should reduce your bet size by 10%, or using my measure of risk your annualised volatility target should come down by one tenth. Long only unleveraged investors don't have to worry about this, it just happens naturally.

In theory this means you can never lose all your money (just 99.999999% of it...!); although this ignores the fact that prices jump and we can't trade continuously.

However you may also be interested in earning a compounded return on your assets. Again Kelly says you'll maximise your expected geometric return (and final account value) if you increase risk capital when you make profits (assuming you weren't targeting a Kelly fraction bet that was too high to begin with). I'll discuss these options in more detail below.

Normally in live trading you'd key your risk capital calculation straight off the brokerage value of your account, which will be more reliable than your back-tested p&l. Future versions of pysystemtrade will include the ability to do that.

Notice that you will need to think about how to handle withdrawals and deposits from your account. If you want to take money out / put money in but keep the same risk then there needs to be some kind of manual adjustment to your account value.

The three methods of capital correction

Fixed capital

This is the trivial case where our capital doesn't change regardless of any losses or gains we make. Here's an example:

Capital	% profit	Profit	Cum profits	Drawdown
100.00	1.00	1.00	1.00	0.00
100.00	-2.00	-2.00	-1.00	2.00
100.00	-1.00	-1.00	-2.00	1.00
100.00	3.00	3.00	1.00	0.00
100.00	1.00	1.00	2.00	0.00
100.00	3.00	3.00	5.00	0.00
100.00	-1.00	-1.00	4.00	1.00

Full compounding

This is the case where we increase capital for losses, and reduce it for gains. Here's an example using the same % profits as above:

Capital	% profit	Profit	Cum profits	Drawdown
100.00	1.00	1.00	1.00	0.00
101.00	-2.00	-2.02	-1.02	0.00
98.98	-1.00	-0.99	-2.01	2.02
97.99	3.00	2.94	0.93	0.99
100.93	1.00	1.01	1.94	0.00
101.94	3.00	3.06	5.00	0.00
105.00	-1.00	-1.05	3.95	0.00
103.95

Half compounding

This is the method that I use. Any losses are used to reduce risk capital. Any gains that bring us up to the point where we recover those losses are used to increase capital. However once we are at the original capital level again we don't increase risk if we go above this. Any further drawdown off the new high water mark (HWM) will mean risk capital is reduced. If you like you can think of this as running a hedge fund with a 100% performance fee.

Capital	% profit	Profit	Cum profits	Drawdown
100.00	1.00	1.00	1.00	0.00
100.00	-2.00	-2.00	-1.00	2.00
98.00	-1.00	-0.98	-1.98	0.98
99.02	3.00	2.97	0.99	0.00
100.00	1.00	1.00	1.99	0.00
100.00	3.00	3.00	4.99	0.00
100.00	-1.00	-1.00	3.99	1.00
99.00

I find it suits me since I live partly off my trading income; I'm not letting it "roll up" for use when I retire. So I have to pay taxes (so I can't use all the income) and because I already run my account at the maximum risk I'm comfortable with. It makes it psychologically easier to be a trader; I can treat my trading account as an investment that periodically and randomly generates a "dividend" in the form of the "performance fee"  (profits over the high water mark); but which otherwise I can't touch. It also means my maximum loss is limited to my notional starting capital. 

It's possible to use a partial compounding method, between half and full compounding. "Three quarter" compounding would mean taking half of any profits generated above the high water mark and adding these to risk capital; losses below the HWM would still impact on capital in their entirety. This might be suitable if for example you wanted to reserve a proportion of your profits to pay taxes. I haven't implemented this.

Capital in pysystemtrade

Quick and dirty

If you are just curious how your account curve will look with compounding, then there is a new method for any account curve type object: .cumulative() which will give you a pandas Series of cumulated returns with a compounding effect. You can plot this, and also run the normal statistical methods, but their results won't be accurate due to the volatility changing over time.

More accurate with positions for live trading

For live trading you are going to need to be able to see what impact your capital correction has on your actual positions.

The existing portfolio object method system.portfolio.get_notional_position outputs notional position, based on the notional fixed capital and risk denoted by the config parameters: percentage_vol_target, base_currency, and notional_trading_capital.
It also calculates some buffers used to reduce over trading with get_buffers_for_position (using the concept of position inertia defined in chapter 11 of my book).

The accounts object now has a new method system.accounts.capital_multiplier(). The capital_multiplier is a number we multiply the notional trading capital by. So if this is just a string of 1.0 then we're using fixed capital. Numbers less than 1.0 indicate we have less capital than we started with, and so on. The function specified by the config parameter capital_multiplier_func (which defaults to syscore.capital.fixed_capital will determine how the multiplier is calculated.

Use syscore.capital.fixed_capital, syscore.capital.full_compounding and syscore.capital.half_compounding as desired.

In live trading I'll eventually be replacing this with a function that uses the actual account value.

Then there are new portfolio methods  get_actual_position and get_actual_buffers_for_position. These return the notional position, and buffers, multiplied by the capital_multiplier. Augmenting the existing accounts method get_buffered_position is get_buffered_position_with_multiplier.

Finally there is a new accounts method system.accounts.portfolio_with_multiplier(). This calculates the p&l of the entire portfolio using the actual positions (rather than the notional positions with fixed capital used by system.accounts.portfolio).

There's some more information in the user guide here.

The three methods with pysystemtrade

To illustrate what's going on with a specific example, here are some plots. In all cases I'm using the standard system from chapter 15 of my book. I've chosen the Eurodollar market as it performs especially well, hence we can see the effect of compounding more clearly. Here's the basic system:


from systems.provided.futures_chapter15.basesystem import futures_system
from matplotlib.pyplot import show

system = futures_system(log_level="on")
system.config.instrument_weights=dict(EDOLLAR=1.0)

Fixed capital

To illustrate what's going on with a specific example, here are some plots. In all cases I'm using the standard system from chapter 15 of my book. I've chosen the Eurodollar market as it performs especially well, hence we can see the effect of compounding more clearly.

Let's start by looking at the p&l with fixed capital

## We don't need this line as it's the default behaviour

system.config.capital_multiplier['func']='syscore.capital.fixed_capital'

system.accounts.portfolio().curve().plot()

show()

So we made about 3 million bucks, but on what capital?

system.accounts.portfolio().capital
Out[19]: 250000.0

This is a scalar, so capital is fixed.

We can also see this as a percentage:

system.accounts.portfolio().percent().curve().plot()

Again we've made just over 10 times our capital. If we wanted to know what our performance was on a cumulative basis then there is the quick and dirty option:

system.accounts.portfolio().cumulative().curve().plot()

... and this is why I dislike looking at compounded graphs. The performance in earlier years is now almost impossible to see. Apparently we could make $300 million trading this thing - that's what compounding $250K for decades at 30% a year will give you. It's a hairy ride however! 

According to t'internet Damian Hirst, who creates art like this, is worth $300 million. I leave you to draw your own conclusions. Source: Guardian.com

Full compounding

Let's introduce a compounding method.

system.config.capital_multiplier['func']='syscore.capital.full_compounding'

First, let's check out the capital multiplier. This is the varying number which we multiply fixed capital by to get variable capital. It starts at 1.0:

system.accounts.capital_multiplier().plot()

Since we're allowing capital to track profits this looks exactly like the line above. We finish with about 1000x as much capital as we started with.

What effect does that have on our p&L:

system.accounts.portfolio_with_multiplier().curve().plot()

Naturally this is exactly like the curve produced above with the 'cumulative()' method. By the way  system.accounts.portfolio_with_multiplier().capital would now give a time series rather than a fixed vale.

So we'll start with $250K and end up $300 million. (or perhaps if you have just $2500 you can see yourself ending up with $3 million).  Okay, yes, at one point in the backtest we drop $400 million, but you can cope with that right? 

What could possibly go wrong?

Well... what about positions? Let's compare the multiplied variable capital, and fixed capital positions:

system.accounts.get_buffered_position_with_multiplier("EDOLLAR", False).plot()

system.accounts.get_buffered_position("EDOLLAR", False).plot()

The barely visible green line is the positions we have with fixed capital. It peaks at about 120 lots. With variable capital we have the blue line, peaking at 300,000 lots. I currently own slightly fewer Eurodollar in the June and September 19 delivery. Total open interest across those two months is about 340,000 lots. In my last job, managing a large portfolio for multi billion dollar quant fund AHL, we never had a position that big. 

At the very least we'd have to do some very serious research on modelling the execution costs associated with turning over that kind of position. At one point we sell 150K lots, pretty much overnight.

The moment the trader realised that selling 150,000 contracts might be a little tricker than he originally thought. Source mirrodaily.com

Half compounding

Finally let's look at the method I use myself, "half compounding", where we ratchet down our risk on losses, but do not increase it beyond the high water mark.

system.config.capital_multiplier['func']='syscore.capital.half_compounding'

Here's the capital multiplier

system.accounts.capital_multiplier().plot()

Notice it is always at, or below 1.0. A value of 0.5 means we are currently in a 50% drawdown.

system.accounts.portfolio_with_multiplier().capital.plot()

Similarly the capital at risk is always equal to the maximum fixed value of $250K, or less.

system.accounts.portfolio_with_multiplier().curve().plot()

Notice that the volatility of the account curve is dampened during the drawdowns.

system.accounts.get_buffered_position_with_multiplier("EDOLLAR", False).plot()

system.accounts.get_buffered_position("EDOLLAR", False).plot()

show()

Positions with fixed capital (green) are always greater than, or equal to, those with variable capital (blue).

We can't plot full compounding and fixed capital together, because the scale would be crazy. But here's the account curves for fixed capital (in blue) and half compounded (in green):

Fixed capital makes more (33.4% a year vs 22.7%) than variable, but with higher risk (annualised risk of 62% vs 43%). The Sharpe comes in very slightly higher (0.54 vs 0.51) and the Sortino a little lower (1.47 vs 1.5). The variable capital has lower average drawdowns (14% vs 20.5%) but we'd expect this given the lower volatility; but also more positive skew of returns (0.77 vs 0.59 on an annual basis) hence the improvement from Sharpe to Sortino.

However this stats are somewhat misleading because the volatility of the variable account curve is non stationary, whereas it's more stable with a fixed account curve (only changing as signals weaken or strengthen).

Half compounding is better in the sense that it's safer and you'll "never" run out of money (jumps aside). But unless your trading strategy is unprofitable you will always end up with less money than with fixed capital; and definitely less than with full compounding.

Conclusion

I hope I've put you off looking at compounded account curves. They have little or no value for system evaluation and understanding. If you want to fantasise about being as rich as Damian Hirst, then feel free but do not bother backtesting the journey.

For actual trading though I recommend you use eithier the full compounding method or half compounding method; both of which you can backtest easily if you wish.

Many traders might fall somewhere between these two stools; letting some of their returns compound but making withdrawals to cover taxes and augment other income. It's hard to backtest this, but in live trading setting your risk capital equal to your account value will ensure you have your risk correct. It will mean however that you will reduce position size when you make withdrawals, possibly incurring transaction costs.